[Reversing] rev-basic-8 문제 풀이

문제

---

rev-basic-8(dreamhack)

정적 분석

---

해당 문제 또한 다른 rev-basic 문제와 동일한 형태이고 분기문인 compare_fun() 만 살펴보면 다음과 같다.

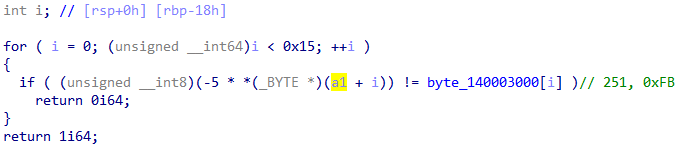
compare_fun()

compare_fun()을 분석하면 입력값인 a1에 -5(0xFB)를 곱한 후 byte_140003000과 비교하는 과정으로 동작한다.

처음 해당 문제를 보았을 때 음수 값인 -5 를 곱하는 것을 보고 막막하기만 하였으나, 자료형을 유심히 보았을 때 해결 방법을 생각할 수 있었다.

a1에 -5를 곱하게 되면 숫자는 4바이트, 문자는 1바이트 이므로 문자의 상위 바이트를 0으로 채운 워 동일한 크기(4 바이트)로 만든 후 곱셈이 이루어진다.

이후 곱셈이 이루어진 결과를 unsigned __int8로 강제 형변환을 한 후 byte_140003000과 비교한다. 이때, 강제형변환을 하는 과정에서 3바이트의 손실이 일어나 하위 1바이트 값만 비교하게 된다.

왜 3바이트의 손실이 발생할까? 기존 a1에 -5를 곱한 값은 4바이트인데 unsigned __int8 자료형의 경우 자료형의 크기가 1바이트이다. 해당 문제와 같이 unsigned __int8로 강제형변환을 할 경우 3바이트의 손실이 발생해 하위 1바이트의 값 남게 된다.

해당 문제를 파악한 후 모듈러연산으로 판단되어 코드를 작성하려고 했으나 브루트포스 방식으로 문제를 해결하면 간단하게 해결될 것 같아서 브루트포스 방식으로 코드를 작성하였다.

최종 코드는 다음과 같다.

dec_list = [172, 243, 12, 37, 163, 16, 183, 37, 22, 198, 183, 188, 7, 37, 2, 213, 198, 17, 7, 197, 0]
result_list = []
for i in range(21):
    for t in range(256):
        if((t * 0xFB) & 0xFF == dec_list[i]):
            result_list.append(t)
    print(chr(result_list[i]), end='')

& 0xFF를 하는 이유 일반적으로 바이트 자료형은 -128 ~ 127 까지 표현되며, 상위 1비트는 음수 및 양수를 판단하는데 사용된다. 그렇기 때문에 0~255까지의 표현이 불가능하다. 이를 해결하기 위해 & 0xFF 연산을 추가적으로 하게 되면 음수 및 양수를 판단하는 비트가 항상 0으로 표현되어 0~255까지의 숫자 표현이 가능해진다.

Flag

---

DH{Did_y0u_brute_force?}

오류, 잘못된 점 또는 궁금한 점이 있으시다면 댓글 남겨주세요❗

Uploaded by N2T